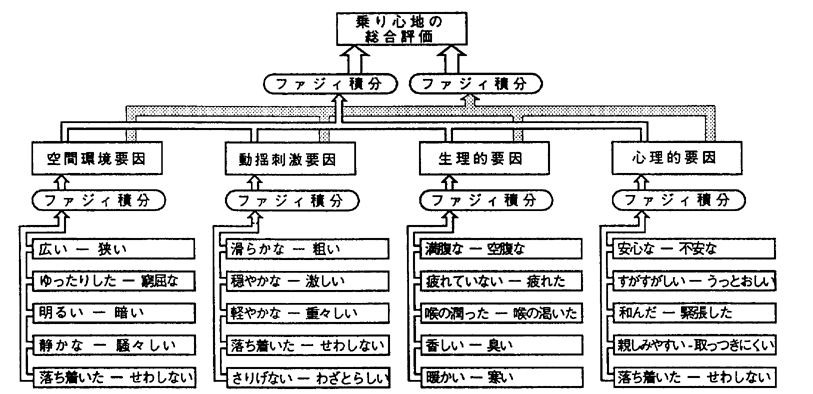
図2.2.3−4階層化ファジィ積分による乗り心地評価

いまE,Fをある可測集合とすると、ファジィ測度は、（3）、（4）式で表される集合関数gで定義される。ここで、E，Fは可測集合を表しており、（3）式は有界性、（4）式は単調性を表している。

ファジィ測度の中でも（3）、（4）式に加え、（5）式で表される加法性を満たすものを確率測度という。

言い換えれば、一般にファジィ測度ではE∩Fのとき、8（EUF）とg（E）+g（F)との関係は、（6）一（8）式の全てが起こり得る。

（6）式は、EとFとの間に相乗効果が働いていることを表しており、（7）式は、EとFとの間に相殺効果が働いていることを表している。また、（g）式は、EとFとの間の相互作用が互いに打ち消しあっているか、互いに独立であることを表しており、確率測度と一致する。このことから、確率測度は、ファジィ測度の特別の場合であるということができる。

このように、単調性のみを満たし、加法性を必要としないファジィ測度を用いて、評価項目の重要度を表現することによって、評価項目間の相互作用を考慮することができ、乗り心地とそれに影響を及ぼす要因との関係を明らかにすることができる。

ファジィ測度で表現した評価項目の重要度をファジィ積分で統合することによって、乗り心地の総合評価を行うことができる。この方法によって、影響度、重要度を推定し、ファジィ測度で表現した

前ページ　　　目次へ　　　次ページ